تعیین مرکز برش در مقاطع جدار نازک باز (مقطع ناودانی)

تعیین مرکز برش در مقاطع جدار نازک باز:

مقطع ناودانی:
اولین تیری که در این مقاله مورد بررسی قرار می دهیم، تیر با مقطع ناودانی است (شکل زیر). بر اساس توضیحات ارائه شده در مبحث «مفهوم مرکز برش»، مرکز برش بر روی محور تقارن (محور z) قرار دارد.

به منظور یافتن موقعیت مرکز برش، محور z را به عنوان محور خنثی در نظر می گیریم و فرض می کنیم که تیر مورد تحلیل، حول این محور خم شده است.

سپس، خط اثر برآیند نیروی برشی Vy را به دست می آوریم. این نیرو، در جهت موازی با محور y اعمال می شود.

به این ترتیب، مرکز برش در محل تقاطع خط اثر Vy با محور z قرار می گیرد. توجه داشته باشید که مبدأ محورها، مرکز هندسی C است.

از این رو، هر دو محور y و z به عنوان محورهای اصلی گذرنده از مرکز هندسی (محورهای اصلی مرکزی) در نظر گرفته می شوند.

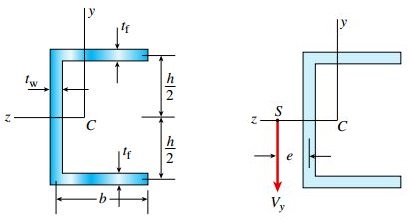
مرکز برش یک مقطع ناودانی (نقطه S)

بر اساس مطالب ارائه شده در مبحث «تحلیل تنش های برشی موجود در تیرهای بال پهن»، تنش های برشی موجود در بال های یک ناودانی به صورت خطی و در جان به صورت سهمی وار تغییر می کنند (شکل زیر).

اگر حداکثر تنش اعمال شده بر بال را با τ1، تنش موجود در بالای جان را با τ2 و حداکثر تنش اعمال شده بر جان را با τmax را تعیین کنیم، امکان محاسبه برآیند تنش های مذکور فراهم می شود.

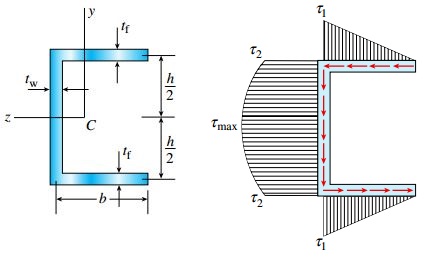
توزیع تنش های برشی در یک مقطع ناودانی

برای تعیین τ1 در بال ابتدا گشتاور اول سطح بال حول محور z را به دست می آوریم:

b: عرض بال؛ tf: ضخامت بال؛ h: ارتفاع تیر

توجه داشته باشید که ابعاد b و h در راستای محور مرکزی مقطع اندازه گیری شده اند. به این ترتیب، تنش τ1 برابر است با:

Iz: ممان اینرسی حول محور z

تنش τ2 در جان تیر نیز مشابه روند بالا (با جایگذاری ضخامت جان در رابطه) محاسبه می شود:

علاوه بر این، گشتاور اول سطح در محور خنثی نیز به صورت زیر به دست می آید:

به این ترتیب، تنش ماکسیمم برابر است با:

تنش های τ1 و τ2 در نیمه پایینی تیر با تنش های مربوطه در نیمه بالایی برابر هستند. با استفاده از نمودارهای تنش (شکل زیر) می توان نیروی برشی افقی F1 در هر دو بال را مورد محاسبه قرار داد.

نیروهای موجود در بال ها با حاصل ضرب مثلث تنش در ضخامت بال برابر هستند:

از آنجایی که هیچ مؤلفه عمودی در نیروهای اعمال شده بر بال وجود ندارد، نیروی عمودی F2 در جان تیر باید با نیروی برشی Vy برابر باشد.

به منظور تأیید صحت محاسبات، تساوی F2=Vy را با استفاده از نمودار تنش در قسمت جان تیر مورد بررسی قرار می دهیم.

نمودار این ناحیه دارای یک قسمت مستطیلی با مساحت τ2h و یک قسمت سهمی وار با مساحت زیر است:

به این ترتیب، نیروی برشی F2 با حاصل ضرب مساحت نمودار برش (مجموع مساحت های دو قسمت) در ضخامت جان tw برابر خواهد بود:

با جایگذاری عبارت های روابط τ2 و τmax در معادله بالا، به معادله زیر می رسیم:

در نهایت، توجه داشته باشید که ممان اینرسی Iz در معادله بالا به صورت زیر محاسبه می شود:

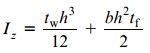
مبنای محاسبات بالا، ابعاد محور مرکزی مقطع است. با جایگذاری عبارت های رابطه Iz در معادله F2 به نتیجه زیر می رسیم:

به این ترتیب، صحت محاسبات انجام شده تأیید می شود. Vy در شکل زیر، برآیند سه نیروی اعمال شده بر سطح مقطع را نمایش می دهد.

این برآیند با محور z متقاطع است و از مرکز برش S می گذرد. بنابراین، گشتاور این نیروها حول هر نقطه دلخواه بر روی سطح مقطع باید با گشتاور نیروی Vy حول آن نقطه برابر باشد.

تعیین رابطه بین گشتاورها، امکان محاسبه مختصات مرکز برشی را فراهم می کند.

برای نمایش مرکز برش بر روی تصویر، آن را به عنوان مرکز گشتاورها در نظر می گیریم. در این حالت، گشتاور حاصل از نیروها برابر با F1h-F2e و نیروی برآیند Vy برابر با صفر خواهد بود.

e، فاصله محور مرکزی جان تا مرکز برش است. با برابر قرار دادن این گشتاورها، به رابطه زیر می رسیم:

با جایگذاری عبارت های روابط F1 و F2 در رابطه بالا و حل معادله به دست آمده بر حسب e، خواهیم داشت:

اگر رابطه به دست آمده برای Iz را در معادله بالا قرار دهیم، به رابطه زیر می رسیم:

به این ترتیب، محل قرارگیری مرکز برش مقطع ناودانی به دست می آید.

با توجه به مطالب ارائه شده در مبحث «مفهوم مرکز برش»، هرگاه نیروهای اعمال شده بر یک تیر ناودانی از مرکز برش آن عبور کنند، آن تیر در معرض خمشِ بدون پیچش قرار می گیرد.

در صورت موازی بودن بارها با محور y و عدم گذر آن ها از مرکز برش (به عنوان مثال، در صورت اعمال بارها در صفحه دربرگیرنده جان)، می توان بارها را با مجموعه ای از نیروهای معادل استاتیکی (از جمله بارهای گذرنده از مرکز برش و کوپل های پیچشی) جایگزین کرد.

در این حالت، ترکیبی از خمش و پیچش درون تیر به وجود می آید. اگر بارهای اعمال شده با محور z هم راستا باشند، یک خمش ساده حول محور y به وجود خواهد آمد.

اگر این بارها به صورت مورب اعمال شوند و از روی مرکز برش عبور کنند، می توان آن ها را با بارهای معادل استاتیکی موازی با محورهای y و z جایگزین کرد.