تحلیل تنش های برشی در تیرهای مستطیلی (رابطه برش)

رابطه برش:
در این بخش، رابطه ای را برای تعیین تنش های برشی τ در یک تیر با مقطع مستطیل می پردازیم.

بررسی تنش های برشی افقی موجود در میان لایه های یک تیر ساده تر از ارزیابی تنش های برشی عمودی اعمال شده بر روی یکی از مقاطع آن است.

برای شروع کار، تیر نمایش داده شده در شکل زیر را در نظر بگیرید. همان گونه که مشاهده می کنید، این تیر تحت خمش غیر یکنواخت قرار دارد. در مرحله بعد، دو مقطع عرضی mn و m1n1 که نسبت به یکدیگر دارای فاصله dx را در نظر بگیرید.

در فاصله میان این دو مقطع، المان mm1n1n تشکیل می شود. گشتاور خمشی و نیروی برشی اعمال شده بر روی صفحه سمت چپ این المان به ترتیب با حروف M و V علامت گذاری شده اند.

امکان تغییر گشتاور خمشی و نیروی برشی بر روی محور تیر وجود دارد.

به همین دلیل، کمیت های صفحه سمت راست المان با عبارت های M+dM و V+dV علامت گذاری می شوند.

به دلیل وجود گشتاورهای خمشی و تنش های برشی در شکل بالا، هر دو سطح المان مورد تحلیل تحت تنش های نرمال و برشی قرار خواهند داشت.

با این وجود، به منظور تعیین رابطه برش فقط به تنش های نرمال نیاز خواهد بود. از این رو، در شکل زیر تنها وضعیت تنش های نرمال موجود در المان mm1n1n نمایش داده شده است.

تنش های نرمال موجود بر روی مقاطع عرضی mn و m1n1 به ترتیب برابرند با:

و

روابط بالا مشابه رابطه خمش هستند. در این روابط، y، فاصله از محور خنثی و I، ممان اینرسی سطح مقطع عرضی حول محور خنثی را نمایش می دهند.

در مرحله بعد، صفحه افقی pp1 را از درون المان mm1n1n عبور می دهیم تا المان کوچک تر mm1p1p مطابق شکل زیر به وجود آید. صفحه pp1 به اندازه y1 از سطح خنثی تیر فاصله دارد.

توجه داشته باشید که به دلیل انطباق سطح بالایی mm1p1p بر روی سطح بالایی تیر، هیچ تنشی بر روی این صفحه وجود نخواهد داشت.

با این وجود، سطح پایینی المان mm1p1p در معرض تنش برشی افقی τ قرار می گیرد. مقاطع عرضی mp و m1p1 نیز به ترتیب تنش های خمشی σ1 و σ2 را تحمل می کنند. این تنش ها توسط گشتاورهای خمشی به وجود می آیند.

علاوه بر این، تنش های برشی عمودی نیز بر روی مقطع عرضی مذکور اعمال می شوند اما هیچ تأثیری بر روی تعادل المان mm1p1p در راستای افقی (بر روی محور x) نمی گذارند.

اگر گشتاورهای خمشی اعمال شده در مقاطع عرضی mn و m1n1 با هم برابر باشند (تیر تحت خمش خالص قرار داشته باشد)، تنش های نرمال σ1 و σ2 بر روی صفحات mp و m1p1 نیز با هم برابر خواهند بود. در این شرایط، المان mm1p1p هنگام اعمال تنش های نرمال در حالت تعادل قرار می گیرد.

به این ترتیب، تنش های برشی τ از روی صفحه پایینی pp1 حذف می شوند. این وضعیت با شرایط تیر تحت خمش خالص مطابقت دارد؛ چراکه در این حالت بارگذاری نیز هیچ نیروی تنشی (در نتیجه هیچ تنش برشی) بر روی تیر اعمال نمی شود.

در صورتی که گشتاورهای خمشی در امتداد محور x تغییر کنند (حالت خمش غیر یکنواخت)، تنش برشی τ اعمال شده بر روی سطح پایینی المان mm1p1p با استفاده از معادلات تعادل در راستای محور x قابل محاسبه خواهد بود.

به این منظور، ابتدا المان سطح dA در فاصله y از محور خنثی را در نظر می گیریم (شکل زیر).

نیروی اعمال شده بر روی این المان برابر با σdA است. پارامتر σ، تنش نرمال را نمایش می دهد. این تنش با استفاده از رابطه خمش به دست می آید.

اگر المان سطح مورد بررسی بر روی سطح سمت چپ mm1p1p قرار داشته باشد (جایی که گشتاور خمشی برابر با M است)، تنش نرمال با استفاده از رابطه σ1=-My/I قابل محاسبه خواهد بود. به این ترتیب، برای المان نیرو داریم:

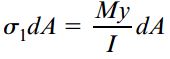
توجه داشته باشید که در معادله بالا تنها از قدر مطلق مقادیر استفاده شده است؛ چراکه جهت تنش ها بر روی شکل مشخص هستند. با جمع المان های نیرو موجود بر روی سطح mp، نیروی افقی کل F1 به دست می آید:

محدوده انتگرال بالا بر روی سطح پر رنگ (از y=y1 تا y=h/2) قرار دارد. در شکل زیر، نیروی F1 بر روی یک نمودار جسم آزاد نمایش داده شده است (از نیروهای عمودی صرف نظر شده است).

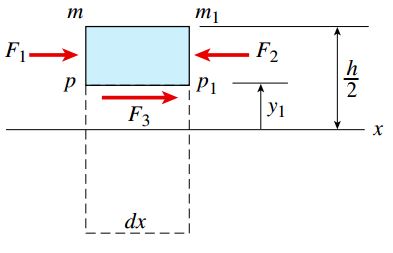
به همین ترتیب، نیروی کل F2 بر روی سطح راست المان (m1p1) نیز به دست می آید:

با تعیین نیروهای F1 و F2، نیروی افقی اعمال شده بر سطح پایینی المان mm1p1p را محاسبه می کنیم. از آنجایی که این المان در حالت تعادل قرار دارد، جمع نیروهای موجود در راستای محور x را به دست می آوریم. به این ترتیب داریم:

یا

کمیت های dM و I بر روی هر سطح مقطع دلخواه دارای مقادیر ثابت هستند. به همین دلیل، این کمیت ها را می توان از انتگرال خارج کرد. به این ترتیب، رابطه F3 به صورت زیر درمی آید:

اگر توزیع تنش های برشی τ بر روی عرض تیر یکنواخت باشد، نیروی F3 برابر است با:

bdx در رابطه بالا، مساحت سطح پایینی المان mm1p1p را نمایش می دهد. با ترکیب این رابطه با رابطه قبلی و حل آن با توجه به پارامتر τ خواهیم داشت:

کمیت dM/dx همان نیروی برشی V است. از این رو، عبارت رابطه بالا به شکل زیر درمی آید:

انتگرال موجود در معادله بالا بر روی بخش پر رنگ مقطع گرفته شده است. به همین دلیل، این انتگرال با گشتاور اول سطح مذکور نسبت به محور خنثی برابری می کند.

به عبارت دیگر، انتگرال بالا، گشتاور اول سطح مقطع بالایی ناحیه ای است که تنش برشی بر روی آن مورد ارزیابی قرار می گیرد. این گشتاور اول معمولاً با حرف Q نمایش داده می شود:

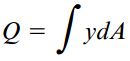
با معرفی مفهوم گشتاور اول، معادله تنش برشی به شکل زیر تبدیل می شود:

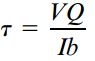
معادله بالا با عنوان «رابطه برش» (Shear Formula) شناخته می شود و به منظور تعیین تنش برشی τ در هر نقطه دلخواه بر روی سطح مقطع یک تیر مستطیلی مورد استفاده قرار می گیرد.

توجه داشته باشید که برای این شکل خاص از سطح مقطع، نیروی برشی V، ممان اینرسی I و عرض b به عنوان کمیت های ثابت در نظر گرفته می شوند.

با این وجود، گشتاور اول Q (و تنش برشی τ) نسبت به فاصله y1 تا محور خنثی تغییر می کند.