نکات تکمیلی تعیین کرنش درون تیرها

نکات تکمیلی تعیین کرنش درون تیرها:
در این مقاله رابطه کرنش-انحنا را تنها با استفاده از هندسه تیر و بدون توجه به خواص رفتاری ماده به دست آوردیم.

از این رو می توانیم نتیجه بگیریم که کرنش های موجود در یک تیر تحت خمش خالص نسبت به فاصله نقطه مورد بررسی از صفحه خنثی به صورت خطی تغییر می کنند و به شکل منحنی تنش-کرنش وابسته نیستند.

وجود اثرات نسبت پواسون، باعث ایجاد کرنش های عرضی (کرنش های نرمال در جهت های x و z) به همراه کرنش های طولی می شود.

اگرچه، به دلیل فراهم بودن امکان تغییر شکل آزادانه در راستای جانبی، هیچ تنش عرضی در تیر به وجود نمی آید.

این وضعیت با شرایط یک تیر منشوری تحت کشش یا فشار مشابه است. به این ترتیب، المان های طولی یک تیر تحت خمش خالص، در معرض تنش تک محوری قرار می گیرند.

مثال:
شکل زیر، یک تیر ساده فولادی با طول L=8ft و ارتفاع h=6ft را نمایش می دهد. بر اثر اعمال کوپل های M0، تیر AB به شکل یک قوس دایره ای و با تغییر مکان رو به پایین δ نسبت به مرکز اولیه خود خم می شود. مقدار کرنش نرمال (افزایش طول) بر روی سطح پایینی تیر برابر با 0.00125 و فاصله بین صفحه خنثی تا این سطح برابر با 3 اینچ است.

با توجه به اطلاعات مسئله، شعاع انحنا ρ، انحنا κ و خمیدگی δ را محاسبه کنید.

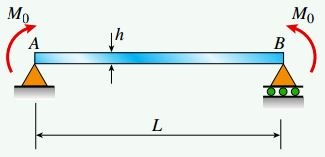
توجه: به دلیل بزرگ بودن طول تیر AB نسبت به ارتفاع آن (L/h=16) و همچنین کرنش بزرگ 0.00125، میزان خمیدگی تیر نسبتاً زیاد خواهد بود. این مسئله تقریباً با شرایط کرنش تسلیم در فولاد سازه ای مطابقت دارد.

انحنا:
به دلیل مشخص بودن مقادیر کرنش طولی در سطح پایینی تیر (εx=0.00125) و فاصله صفحه خنثی تا این سطح (y=-3in)، می توان از رابطه زیر برای تعیین شعاع انحنا و انحنای تیر استفاده کرد.

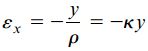
اگر رابطه بالا را بر حسب ρ بازنویسی کرده و مقادیر عددی را درون آن جایگذاری کنیم، خواهیم داشت:

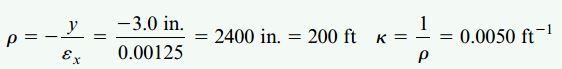
این نتیجه نشان می دهد که شعاع انحنای تیر نسبت به طول آن بسیار بزرگ است. با وجود بزرگ بودن میزان کرنش، مقدار عددی به دست آمده غیر منطقی به نظر می رسد.

خمیدگی:
با توجه به مطالب ارائه شده در مبحث «انحنای تیر و مفاهیم مرتبط با آن»، اعمال یک گشتاور خمشی ثابت (خمش خالص) باعث ایجاد انحنای ثابت بر روی طول تیر می شود.

از این رو، منحنی تغییر شکل تیر به شکل یک قوس دایره ای درمی آید. بر اساس شکل زیر، فاصله مرکز انحنا ‘O تا مرکز تغییریافته تیر ‘C با شعاع انحنا ρ و فاصله ‘O تا نقطه C بر روی محور x با ρcosθ برابر است (θ، زاویه BO’C را نمایش می دهد).

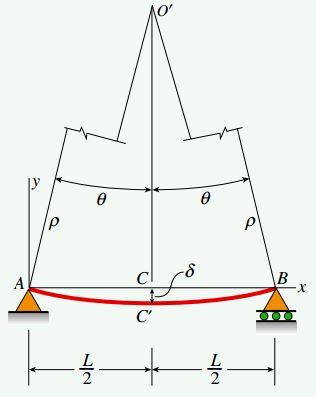
به این ترتیب، میزان خمیدگی در نقطه مرکزی تیر با استفاده از رابطه زیر به دست می آید:

اگر شکل منحنی خمیدگی نزدیک به یک خط راست باشد، فاصله بین تکیه گاه ها را با طول تیر برابر در نظر می گیریم. در نتیجه، رابطه زیر در مثلث BO’C برقرار می شود:

با جایگذاری مقادیر عددی در رابطه بالا، خواهیم داشت:

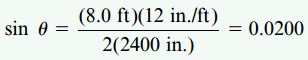
و

در مسائل واقعی، به دلیل کوچک بودن زاویه θ، عبارت sinθ را با مقدار θ (بر حسب رادیان) برابر در نظر گرفته می شود.

در صورت جایگذاری زاویه θ در رابطه ρ، میزان خمیدگی تیر به دست می آید:

این خمیدگی نسبت به طول تیر بسیار کوچک است. اگر بخواهیم این نسبت را به صورت عددی بیان کنیم:

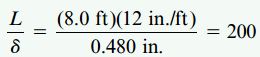
این مسئله نشان می دهد که علیرغم بزرگ بودن مقدار کرنش های به وجود آمده، منحنی خمیدگی تیر تقریباً صاف خواهد بود.

توجه داشته باشید که به منظور نمایش بهتر شرایط مسئله، منحنی خمیدگی نمایش داده شده در شکل های بالا به صورت اغراق آمیز به تصویر کشیده شده است.

توجه: هدف از تشریح این مسئله، نمایش مقادیر شعاع انحنا و خمیدگی تیر نسبت به طول آن بود.

اگرچه به دلیل فرض خمش خالص و دایره ای بودن شکل منحنی خمیدگی، روش مورد استفاده برای تعیین خمیدگی تیر یک مقدار تقریبی را ارائه داد.