تنش های موجود بر روی صفحات مورب

تنش های موجود بر روی صفحات مورب:
اکنون می توانیم تنش های اعمال شده بر روی صفحات مورب المان های تحت برش خالص را تعیین کنیم.

روش اتخاذ شده در این بخش همانند مطالب ارائه شده در مبحث «آشنایی با نحوه تعیین مؤلفه های تنش بر روی صفحات مورب» است.

برای شروع تحلیل، المان دوبعدی زیر را در نظر بگیرید. رسم المان دوبعدی به منظور سادگی تحلیل صورت می گیرد.

باید توجه داشته باشید که المان مورد بررسی در راستای عمود بر صفحه نیز دارای بعد (ضخامت) است.

در مرحله بعد، المان مربعی را تحت زاویه θ نسبت به محور x برش می دهیم (شکل زیر). به این ترتیب، یک المان تنش گوه ای (مثلثی) به وجود می آید.

تنش های نرمال (σθ) و برشی (τθ) بر روی صفحه مورب این المان اعمال می شوند.

قواعد علامت گذاری برای تنش های برشی اعمال شده بر روی صفحات مورب (τθ) با قواعد علامت گذاری برای تنش های برشی اعمال شده بر روی صفحات یک المان مکعبی (τ) متفاوت است.

اگر جهت تنش برشی موجود بر روی صفحات مورب به صورت ساعت گرد باشد، علامت آن مثبت در نظر گرفته خواهد شد.

علاوه بر این، علامت مثبت برای تنش های نرمال کششی و علامت منفی برای تنش های نرمال فشاری مورد استفاده قرار می گیرد.

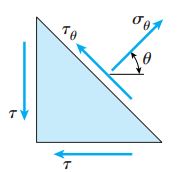
با توجه به نکات ارائه شده، صفحات عمودی و افقی المان مثلثی بالا دارای تنش های برشی مثبت و صفحه مورب آن دارای تنش های نرمال و برشی مثبت خواهند بود.

اکنون با در نظر گرفتن تعادل المان مثلثی می توانیم تنش های σθ و τθ را تعیین کنیم. نیروهای اعمال شده بر روی هر صفحه از حاصل ضرب تنش در مساحت به دست می آید.

به عنوان مثال، نیروی اعمال شده بر روی صفحه سمت چپ با حاصلِ τA0 برابر است. A0، مساحت صفحه عمودی را نمایش می دهد.

با توجه به نمودار جسم آزاد نمایش داده شده در شکل زیر، این نیرو در جهت منفی محور y اعمال می شود.

به دلیل ثابت بودن ضخامت المان در راستای z، مساحت صفحه پایینی از رابطه A0tanθ و مساحت صفحه مورب از رابطه A0secθ به دست می آید.

با ضرب تنش های موجود در مساحت صفحات دربرگیرنده آن ها و تعیین نیروهای باقیمانده، نمودار جسم آزاد المان مثلثی کامل می شود.

پس از رسم نمودار جسم آزاد می توانیم دو معادله تعادل را برای المان مثلثی بنویسیم.

معادله اول در جهت σθ و معادله دوم در جهت τθ خواهد بود. در هنگام نوشتن این معادلات باید نیروهای موجود بر روی صفحات سمت چپ و پایین المان را به مؤلفه های هم جهت با σθ و τθ تجزیه کنیم.

به این ترتیب با جمع نیروهای موجود در راستای σθ، خواهیم داشت:

یا

معادله دوم از جمع نیروهای موجود در راستای τθ به دست می آید:

یا

با استفاده از روابط مثلثاتی می توانیم این معادلات را به فرم ساده تری بازنویسی کنیم:

با استفاده از معادلات بالا، امکان محاسبه تنش های نرمال و برشی اعمال شده بر روی صفحه مورب، با توجه به مقادیر تنش برشی τ بر روی صفحات x و y و زاویه θ فراهم می شود.

شکل زیر، نحوه تغییرات تنش های σθ و τθ نسبت به زاویه θ را در قالب یک نمودار نمایش می دهد.

با توجه به این نمودار، مقدار تنش نرمال و برشی در صفحه سمت راست المان تنش (θ=0) به ترتیب برابر با σθ=0 و τθ=τ است.

به دلیل اعمال پادساعت گرد تنش برشی τ، علامت تنش برشی τθ باید مثبت باشد. این موضوع با علامت نمایش داده شده در نمودار مطابقت دارد.

برای صفحه بالایی المان (θ=90)، مقادیر تنش برابر با σθ=0 و τθ=-τ خواهند بود. علامت منفی در τθ، بیانگر ساعت گرد بودن جهت اعمال این تنش است.

توجه داشته باشید که بزرگ ترین مقادیر عددی تنش های برشی در زوایای θ=0 و θ=90 و همچنین صفحات مقابل آن ها، یعنی θ=180 و θ=270 رخ می دهند.

با توجه به نمودار، تنش نرمال σθ در زاویه θ=45 به مقدار ماکسیمم خود می رسد. در این زاویه، تنش نرمال دارای علامت مثبت (کشش) و مقدار عددی τ است. به همین ترتیب، σθ در زاویه θ=-45 به مقدار مینیمم خود می رسد.

در این زاویه، تنش مذکور دارای علامت منفی (فشار) و مقدار عددی τ- است. مقدار تنش برشی τθ در هر دو زاویه 45 برابر با صفر خواهد بود.

شکل زیر، المان تنش دوران یافته تحت زوایای θ=0 و θ=45 را نمایش می دهد. بر اساس این شکل، المان دوران یافته تحت زاویه 45 درجه در معرض تنش های کششی و فشاری برابر قرار دارد. تنش های کششی در راستای عمود بر تنش های فشاری اعمال می شوند.

به علاوه، هیچ تنش برشی در این المان به وجود نمی آید.

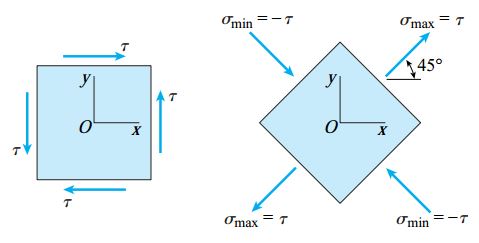
توجه داشته باشید که تنش های نرمال اعمال شده بر روی المان دوران یافته (شکل سمت راست) در اثر اعمال تنش های برشی τ بر روی المان اولیه (شکل سمت چپ) به وجود می آیند.

در صورتی که جهت اعمال تنش های برشی المان اولیه برعکس شود، جهت تنش های نرمال المان دوران یافته نیز تغییر خواهد کرد.

اگر یک المان تنش تحت زاویه ای به غیر از 45 دوران کند، هم تنش های نرمال و هم تنش های برشی بر روی صفحات مورب آن اعمال خواهند شد.

معادلات این بخش برای المان های تنش در حالت برش خالص معتبر هستند و به نوع سازه مورد بررسی بستگی ندارند.

به علاوه، این معادلات برای تمام مواد (الاستیک یا غیر الاستیک، خطی یا غیر خطی) کاربرد دارند؛ چراکه به منظور تعیین آن ها تنها از معادلات تعادل کمک گرفته شده است.

در هنگام اعمال بارهای پیچشی، ترک های ایجاد شده در مواد شکننده و مواد دارای مقاومت کششی پایین به صورت یک مارپیچ 45 درجه ای گسترش می یابند.

علت این امر، وجود تنش های کششی ماکسیمم بر روی صفحاتی است که تحت زاویه 45 درجه دوران یافته اند.

این رفتار را می توان در هنگام پیچاندن یک تکه گچ کلاسی به خوبی مشاهده کرد (مانند شکل زیر).