کاربرد معادلات تبدیل:
معادلات تبدیل تنش بر روی صفحه xy را می توان در صورت وجود تنش نرمال σz نیز مورد استفاده قرار داد. دلیل این امر، عدم حضور σz در معادلات تعادل مورد استفاده برای تبدیلات تنش است.
بنابراین، معادلات تبدیل تنش صفحه ای برای تنش های موجود در حالت کرنش صفحه ای نیز کاربرد دارند. این معادلات عبارت اند از:
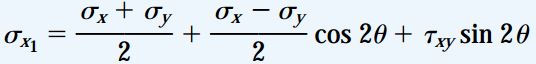
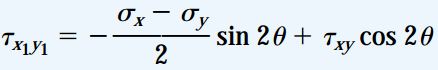
این شرایط برای حالت کرنش صفحه ای نیز صدق می کند. به این ترتیب، با تعیین معادلات تبدیل کرنش برای حالت کرنش صفحه ای در صفحه xy، این معادلات در صورت وجود کرنش εz نیز قابل استفاده خواهند بود.
این موضوع دلیل ساده ای دارد. کرنش εz در رابطه هندسی به کار رفته برای تعیین معادلات تبدیل تأثیرگذار نیست.
بنابراین، معادلات تبدیل کرنش صفحه ای را می توان برای کرنش های موجود در حالت تنش صفحه ای نیز به کار برد.
در نهایت، باید به خاطر داشته باشید که معادلات تبدیل تنش صفحه ای تنها با استفاده از معادلات تعادل به دست می آیند و به همین خاطر برای تمام مواد (الاستیک یا غیر الاستیک) قابل استفاده هستند. معادلات تبدیل کرنش صفحه ای نیز همین شرایط را دارند.
این معادلات تنها با استفاده از روابط هندسی به دست می آیند و به همین دلیل مستقل از خواص ماده هستند.
مراحل تعیین معادلات تبدیل کرنش صفحه ای:
به منظور تعیین معادلات تبدیل کرنش صفحه ای، از محورهای مختصات نمایش داده شده در شکل زیر کمک می گیریم.
در ابتدا فرض می کنیم که مقادیر کرنش های نرمال εx و εy به همراه کرنش برشی γxy بر روی محورهای xy مشخص هستند. با استفاده از این مقادیر، روابط مورد نیاز برای تعیین کرنش نرمال εx1 و کرنش برشی γx1y1 بر روی محورهای x1y1 را به دست می آوریم.
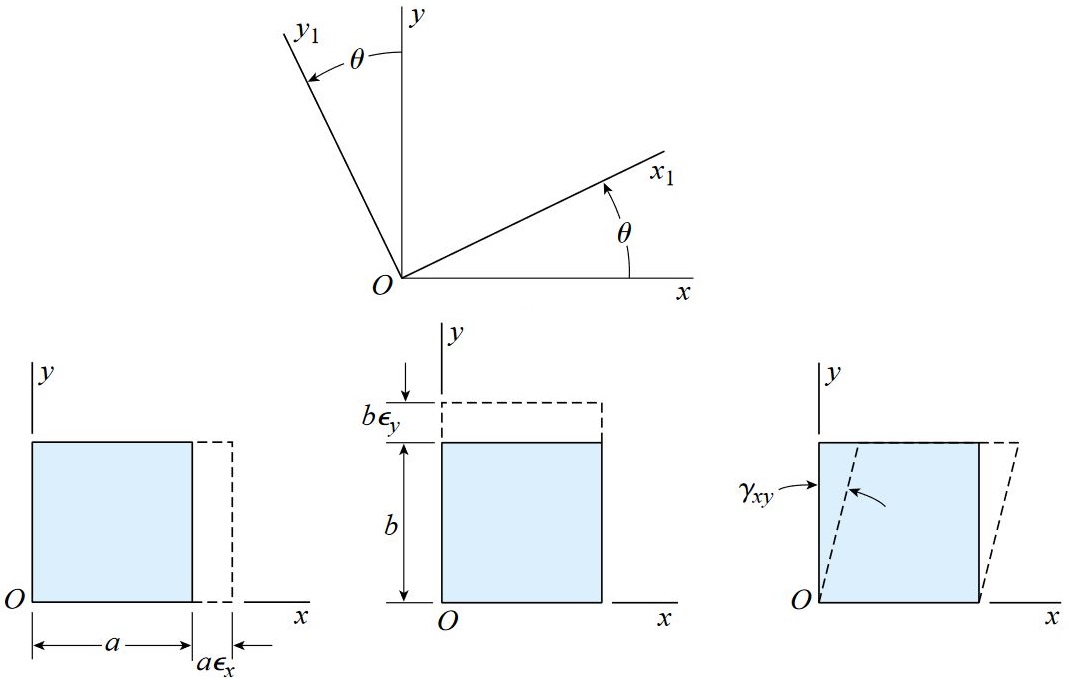
محورهای x1y1 تحت زاویه θ نسبت به محورهای xy و به صورت ساعت گرد دوران یافته اند. توجه داشته باشید که با جایگذاری θ+90 به جای θ در معادله εx1، معادله جداگانه ای برای تعیین کرنش نرمال εy1 به دست می آید.
کرنش نرمال εx1:
به منظور تعیین کرنش نرمال εx1 در راستای x1، یک المان کوچک از ماده را مطابق شکل زیر به گونه ای در نظر می گیرم که محور x1 بر روی قطر صفحه z و محورهای x و y بر روی اضلاع آن قرار گرفته باشند. این شکل، یک نمای دوبعدی از المان مورد نظر را نمایش می دهد (راستای z به سمت داخل صفحه است).
برای شروع تحلیل، کرنش εx در راستای x را در نظر بگیرید. این کرنش باعث ایجاد تغییر طولی به اندازه εxdx در راستای محور x می شود. dx، طول ضلع المان در جهت مورد نظر را نمایش می دهد (شکل بالا). با ایجاد این تغییر طول، قطر المان به اندازه رابطه زیر افزایش می یابد:
اکنون، کرنش εy در راستای y را در نظر بگیرید. این کرنش باعث ایجاد تغییر طولی به اندازه εydy در راستای محور y می شود. dy، طول ضلع المان در جهت مورد نظر را نمایش می دهد (شکل زیر).
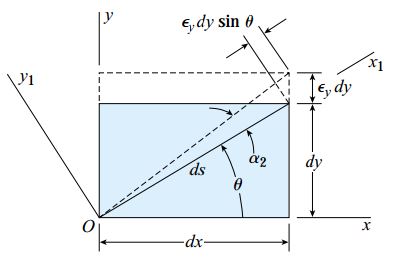
با ایجاد این تغییر طول، قطر المان به اندازه رابطه زیر افزایش می یابد:
در نهایت، کرنش برشی γxy در صفحه xy را در نظر بگیرید. این کرنش باعث ایجاد انحراف المان می شود. این انحراف، زاویه گوشه پایین چپ المان را به اندازه کرنش برشی کاهش می دهد. به این ترتیب، صفحه بالایی المان نسبت به صفحه پایینی به اندازه γxydy به سمت راست حرکت می کند (شکل زیر).
تغییر شکل به وجود آمده باعث افزایش قطر المان به اندازه رابطه زیر می شود:
افزایش کلی طول قطر (Δd) از جمع سه عبارت قبلی به دست می آید:
کرنش نرمال εx1 در راستای x1 از تقسیم افزایش طول قطر المان (Δd) بر طول اولیه آن (ds) به دست می آید:
از آنجایی که dx/ds=cosθ و dy/ds=sinθ، معادله تبدیل کرنش نرمال به صورت زیر خواهد بود:
بنابراین، در این بخش به معادله ای دست یافتیم که میزان کرنش نرمال در راستای x1 را با توجه به پارامترهای εy، εx و γxy محاسبه می کند. همان گونه که قبلاً نیز به آن اشاره شد، با جایگذاری θ+90 به جای θ در معادله εx1، رابطه جداگانه ای برای تعیین کرنش نرمال εy1 به دست می آید.
کرنش برشی γx1y1:
اکنون کرنش برشی γx1y1 در صفحه x1y1 را مورد تحلیل قرار می دهیم. این کرنش با میزان کاهش زاویه بین محورهای x1 و y1 برابر است.
برای درک بهتر این تحلیل، شکل زیر را در نظر بگیرید. این شکل، علاوه بر محورهای x1y1، محورهای xy را نیز نمایش می دهد.
این دو دستگاه مختصات به اندازه زاویه θ با یکدیگر اختلاف دارند. تغییر شکل های ناشی از کرنش های εy، εx و γxy باعث دوران پادساعت گرد خط Oa به اندازه زاویه α نسبت به محور x1 می شود.
به همین ترتیب، خط Ob که در ابتدا بر روی محور y1 قرار داشت، به دلیل تغییر شکل های به وجود آمده تحت زاویه β به صورت ساعت گرد دوران می کند.
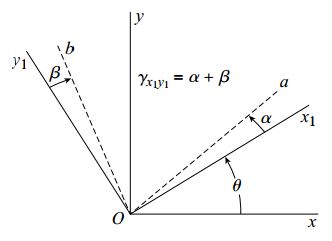
کرنش برشی γx1y1، کاهش زاویه بین دو خط Oa و Ob را نمایش می دهد. به این ترتیب:
بنابراین، به منظور یافتن کرنش برشی γx1y1، در ابتدا باید زوایای α و β را تعیین کنیم. زاویه α از طریق تغییر شکل های نمایش داده شده در شکل زیر قابل محاسبه است. کرنش εx باعث دوران ساعت گرد قطر المان می شود.
زاویه این دوران را با حرف α1 مشخص می کنیم. با توجه به شکل زیر، مقدار زاویه α1 از تقسیم εxdxsinθ بر طول قطر (ds) به دست می آید:
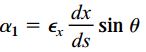
به همین ترتیب، کرنش εy باعث دوران پادساعت گرد قطر المان تحت زاویه α2 می شود. با توجه به شکل زیر، مقدار زاویه α2 از تقسیم εydycosθ بر طول قطر (ds) قابل محاسبه است:
در نهایت، کرنش γxy باعث دوران ساعت گرد قطر المان تحت زاویه α3 می شود. با توجه به شکل زیر، مقدار این زاویه از تقسیم γxydysinθ بر ds به دست می آید:
بنابراین، برآیند دورانِ پادساعت گرد قطر که در تصویر زیر نمایش داده شده است، از جمع زوایای α2، α1 و α3 حاصل می شود:
با توجه به اینکه dx/ds=cosθ و dy/ds=sinθ، رابطه بالا را می توان به صورت زیر بازنویسی کرد:
خط Ob در ابتدا به اندازه 90 درجه نسبت به خط Oa اختلاف داشت. به این ترتیب، با جایگذاری θ+90 به جای θ در معادله α، رابطه ای برای تعیین مقدار زاویه دوران این خط (β) به دست می آید. دوران زاویه α به صورت پادساعت گرد و مثبت در نظر گرفته شده است. از این رو، به دلیل ساعت گرد بودن دوران زاویه β، علامت آن منفی خواهد بود. بنابراین داریم:
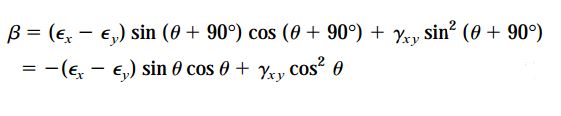
با اضافه کردن روابط مربوط به α و β در معادله کرنش برشی γx1y1 خواهیم داشت:
به منظور تبدیل معادله بالا به یک فرم کاربردی تر، تمام عبارات آن را تقسیم بر 2 می کنیم:
به این ترتیب در این بخش به معادله ای دست یافتیم که می تواند میزان کرنش برشی γx1y1 نسبت به محورهای x1y1 را با توجه به پارامترهای εy، εx و γxy محاسبه کند.
معادلات تبدیل کرنش صفحه ای:
با استفاده از روابط مثلثاتی زیر می توان معادلات ارائه شده در بخش های قبل را با توجه به پارامتر 2θ بازنویسی کرد:
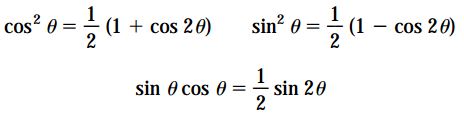
با در نظر گرفتن این روابط مثلثاتی، معادلات تبدیل کرنش صفحه ای به فرم زیر درمی آیند:
و
با مقایسه پارامترهای موجود در معادلات تبدیل کرنش صفحه ای و معادلات تبدیل تنش صفحه ای می توان مشاهده کرد که پارامتر εx1 معادل σx1، عبارت γx1y1/2 معادل τx1y1، پارامتر εx معادل σx، پارامتر εy معادل σy و عبارت γxy/2 معادل τxy است.
جدول زیر، متغیرهای مشابه در هر یک از این دو معادلات تبدیل را نمایش می دهد:
تنش و کرنش:
تشابه بین معادلات تبدیل کرنش صفحه ای و معادلات تبدیل تنش صفحه ای نشان می دهد که تمامی مفاهیم ارائه شده در حالت تنش صفحه ای دارای مفاهیم معادل در حالت کرنش صفحه ای هستند. به عنوان مثال، حاصل جمع کرنش های نرمال در جهت های عمود بر هم مقداری ثابت است:
رابطه بالا را با رابطه ارائه شده در مبحث تنش های نرمال مقایسه کنید:
با جایگذاری متغیرهای معادل (در جدول بالا) می توان تشابه بین مفاهیم کرنش صفحه ای و تنش صفحه ای را به راحتی مشاهده کرد. در ادامه به معرفی برخی از معادلات مشابه دیگر در حالت کرنش صفحه ای می پردازیم.
|
|
|
|
| نماد اعتماد الکترونیک | نشان ملی ثبت | گواهی شامد ارشاد |
© کلیه حقوق مادی و معنوی این وب سایت متعلق به داده پردازان هومان پویان می باشد.
