تنش های موجود بر روی یک المان دوران یافته در دایره مور

تنش های موجود بر روی یک المان دوران یافته در دایره مور:
اکنون تنش های اعمال شده بر روی صفحات المان دوران یافته تحت زاویه θ نسبت به محور x یعنی تنش های σy1، σx1 و τx1y1 را در نظر می گیریم.

اگر زاویه θ مشخص باشد، تنش های مذکور با استفاده از دایره مور قابل تعیین خواهند بود.

به این منظور، ابتدا به اندازه 2θ از شعاع CA در جهت پادساعتگرد حرکت می کنیم و نقطه D با مختصات σx1 و τx1y1 را بر روی دایره علامت می زنیم.

نقطه D، تنش های موجود بر روی صفحه x1 در المان نمایش داده شده در شکل بالا را نمایش می دهد.

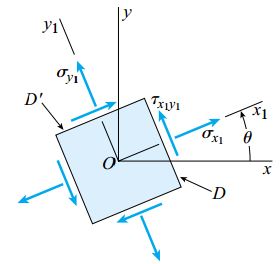
توجه داشته باشید که زاویه 2θ بر روی دایره مور با زاویه θ بر روی المان تنش برابر است.

به عنوان مثال، نقطه D بر روی دایره مور به اندازه 2θ با نقطه A اختلاف دارد اما اختلاف زاویه صفحه x1 با صفحه x بر روی المان به اندازه θ است (شکل بالا و پایین را با هم مقایسه کنید).

به منظور نمایش تطابق بین مختصات نقطه D بر روی دایره مور (σx1,τx1y1) و معادلات تبدیل تنش صفحه ای از هندسه دایره کمک می گیریم. به این منظور، ابتدا زاویه بین خط CD و محور σx1 با حرف β نمایش می دهیم. سپس، با توجه به هندسه دایره روابط زیر را برای تعیین مختصات نقطه D به دست می آوریم:

توجه داشته باشید که زاویه بین شعاع CA و محور افقی مختصات برابر با 2θ+β است. بنابراین:

با بسط سینوس و کسینوس به روابط زیر می رسیم:

با ضرب cos2θ در رابطه اول، ضرب sin2θ در رابطه دوم و جمع این دو رابطه با هم خواهیم داشت:

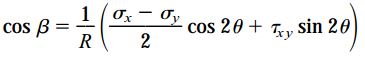
با ضرب sin2θ در رابطه اول، ضرب cos2θ در رابطه دوم و تفریق این دو رابطه از هم نیز خواهیم داشت:

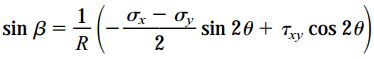
اگر روابط cosβ و sinβ را در روابط اول و دوم جایگذاری کنیم، به معادلات تبدیل σx1 و τx1y1 می رسیم. بنابراین، نقطه D با زاویه 2θ بر روی دایره مور، وضعیت تنش بر روی صفحه x1 با زاویه θ بر روی المان را نمایش می دهد.

نقطه ‘D در مقابل نقطه D قرار دارد. اختلاف زاویه بین نقاط 180 درجه است. بنابراین، نقطه ‘D بر روی دایره، تنش های موجود بر روی صفحه ای با اختلاف 90 نسبت به نقطه D بر روی المان تنش را نمایش می دهد.

به این ترتیب، مختصات نقطه ‘D بر روی دایره مور، بیانگر مقادیر تنش های σy1 و τx1y1 بر روی صفحه y در المان تنش است (شکل های بالا و پایین را با هم مقایسه کنید).

در این بخش، به معرفی نحوه نمایش مؤلفه های تنش بر روی نقاط دایره مور و ارتباط آن ها با تنش های اعمال شده بر روی یک المان پرداختیم. تنش های موجود بر روی یک المان دوران یافته تحت زاویه θ توسط مختصات نقطه ای با اختلاف زاویه 2θ نسبت به نقطه مرجع (A) بر روی دایره مور مشخص می شوند.

بنابراین، با دوران محورهای x1y1 تحت زاویه θ در جهت پادساعتگرد، نقطه مربوط به صفحه x1 به اندازه 2θ در جهت پادساعتگرد بر روی دایره مور حرکت می کند.

به همین ترتیب، در صورت دوران محورهای مختصات به اندازه یک زاویه مشخص در جهت ساعتگرد، نقطه مورد بررسی بر روی دایره مور به اندازه دو برابر آن زاویه در جهت ساعتگرد حرکت خواهد کرد.

تنش های اصلی:
تعیین تنش های اصلی به عنوان مهم ترین کاربرد دایره مور محسوب می شود. توجه داشته باشید که در نقطه P1 بر روی دایره مور، تنش نرمال به بیشترین مقدار خود و تنش برشی به کمترین مقدار خود (صفر) می رسد.

از این رو، نقطه P1 یکی از تنش های اصلی و یکی از صفحات اصلی را نمایش می دهد. طول نقطه P1، به عنوان مقدار تنش اصلی بزرگ (σ1) و زاویه آن نسبت به نقطه مرجع (2θp1)، به عنوان جهت گیری صفحه اصلی در نظر گرفته می شود.

صفحه اصلی مربوط به تنش اصلی کوچک نیز با نقطه P2 و در مقابل نقطه P1 بر روی دایره مشخص می شود.

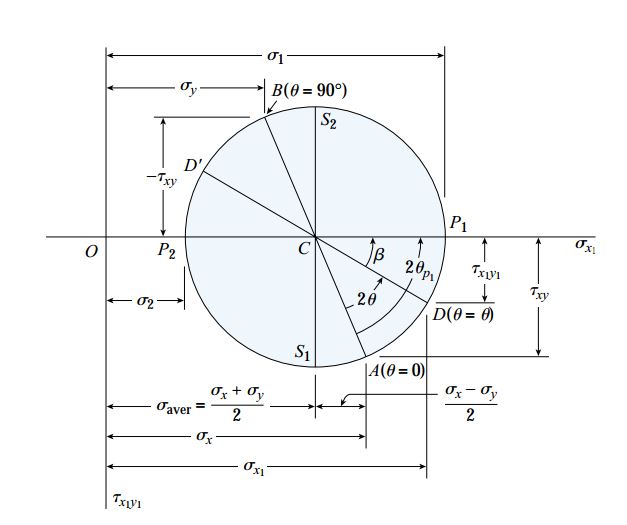
بر اساس هندسه دایره مور، تنش اصلی بزرگ برابر است با:

با جایگذاری رابطه R در رابطه بالا، معادله زیر به دست می آید:

به همین ترتیب می توان مطابقت بین معادله σ2 با روابط هندسی موجود بر روی دایره مور را تأیید کرد. زاویه اصلی بین محور x و صفحه تنش اصلی بزرگ در المان تنش (θp1)، نصفِ زاویه بین خطوط CA و CP1 بر روی دایره مور (2θp1) است.

با بررسی دایره می توان روابط زیر را بین کسینوس و سینوس زاویه 2θp1 با پارامترهای تنش مشاهده کرد:

این روابط با روابط به دست آمده از معادلات تعادل تنش صفحه ای یکسان هستند.

بنابراین، روابط هندسی به دست آمده از دایره مور در این مورد نیز با معادلات تعادل مطابقت دارند. توجه داشته باشید که اختلاف بین زاویه اصلی 2θp2 با 2θp1 بر روی دایره مور 180 درجه است. بنابراین، رابطه θp2=θp1+90 در اینجا نیز برقرار خواهد بود.