سازه های نامعین استاتیکی

سازه های نامعین استاتیکی:
در یک سازه نامعین استاتیکی که از مواد الاستو پلاستیک ساخته شده است، تحلیل رفتار سازه پیچیده تر می شود.

هنگام رخ دادن تسلیم در یکی از عضوهای این نوع سازه، عضوهای دیگر در برابر هرگونه افزایش بار مقاومت می کنند.

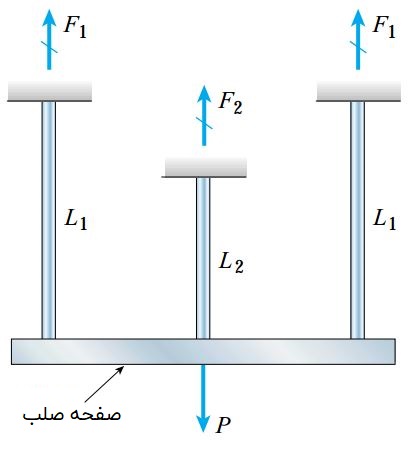
با ادامه افزایش میزان بار و تسلیم عضوهای بیشتر، کل سازه در معرض تسلیم قرار می گیرد. برای آشنایی با رفتار یک سازه نامعین استاتیکی، تصویر زیر را در نظر بگیرید.

این سازه از سه میله فولادی متصل به یک صفحه صلب تشکیل شده است. بار P به صفحه صلب اعمال می شود. طول دو میله کناری L1 و طول میله میانی L2 است. هر سه میله دارای سطح مقطع یکسان هستند.

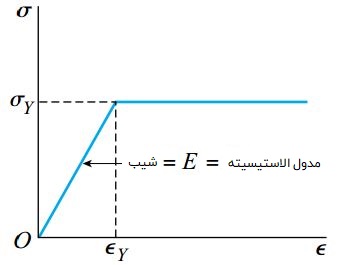
شکل زیر، منحنی تنش-کرنش ایده آل برای فولاد تشکیل دهنده میله های سازه بالا را نمایش می دهد. مدول الاستیسیته در ناحیه الاستیک خطی برابر با E=σY/εY است.

تحلیل سازه های نامعین استاتیکی، با تعیین معادلات تعادل و سازگاری شروع می شود. با توجه به تعادل صفحه صلب در راستای عمودی داریم:

F1: نیروی محوری در میله های کناری؛ F2: نیروی محوری در میله میانی

با شروع بارگذاری، صفحه صلب به سمت پایین حرکت می کند. به این ترتیب، معادله سازگاری به صورت زیر خواهد بود:

δ1: تغییر طول میله های کناری؛ δ2: تغییر طول میله میانی

روابط بالا تنها به تعادل و هندسه سازه بستگی دارند. به همین دلیل، این روابط برای تمامی مقادیر P معتبر هستند و به قرارگیری کرنش در ناحیه الاستیک خطی یا ناحیه پلاستیک وابسته نیستند.

در صورت کوچک بودن بار P، میزان تنش های موجود در میله ها کم تر از تنش تسلیم σY خواهد بود و ماده در محدوده الاستیک خطی قرار خواهد گرفت. بنابراین، رابطه نیرو-جابه جایی (رابطه بین نیروها و تغییر شکل های به وجود آمده) به صورت زیر بیان می شود:

با جایگذاری روابط بالا در معادلات سازگاری، داریم:

با حل هم زمان روابط بالا و معادلات تعادل، به روابط زیر می رسیم:

به این ترتیب، نیروهای درون میله ها در محدوده الاستیک خطی تعیین می شوند. مقادیر تنش های حاصل از این نیروها نیز با استفاده از روابط زیر به دست می آیند:

معادلات به دست آمده برای نیروها و تنش ها در صورتی قابل استفاده هستند که تنش های درون هر سه میله زیر حد تسلیم قرار داشته باشند.

با افزایش تدریجی بار P تا لحظه رخ دادن تسلیم در یکی از میله ها (میله های کناری یا میله داخلی)، تنش های درون میله ها افزایش می یابند.

فرض کنید که مطابق شکل زیر میله های کناری از میله میانی بلندتر باشند. در این وضعیت، تنش های ایجاد شده در میله میانی نسبت به میله های کناری بیشتر است. به این ترتیب، میله میانی زودتر از دو میله دیگر به تنش تسلیم می رسد.

با رسیدن به نقطه تسلیم، نیروی درون میله میانی F2=σYA خواهد بود. مقدار بار P در هنگام رسیدن هر یک از میله ها به تنش تسلیم با عنوان بار تسلیم (PY) شناخته می شود.

با قرار دادن σYA در روابط مربوط به محاسبه نیروها، مقدار PY از طریق رابطه زیر تعیین می شود:

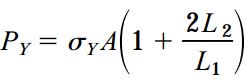
تا زمانی که بار P کمتر از PY باشد، سازه به صورت الاستیک خطی رفتار می کند و روابط ارائه شده برای محاسبه نیروها قابل استفاده هستند.

جابه جایی رو به پایین میله در بار تسلیم با عنوان جابه جایی تسلیم (δY) شناخته می شود. این جابه جایی با تغییر طول میله میانی در هنگام رسیدن به تنش تسلیم برابر است:

شکل زیر، رابطه بین بار اعمال شده P و جابه جایی δ در منحنی بار-جابه جایی سازه بالا را نمایش می دهد. خط OA، بیانگر رفتار سازه تا لحظه رسیدن به تنش تسلیم PY است. با افزایش بار پس از نقطه A، نیروهای F1 در میله های کناری افزایش می یابند اما نیروی F2 در میله میانی در مقدار σYA ثابت باقی می ماند؛ چراکه این میله اکنون به صورت پلاستیک کامل رفتار می کند.

هنگامی که نیروهای F1 به مقدار σYA می رسند، میله های کناری نیز تسلیم می شوند و در نتیجه، مقاومت سازه در برابر تحمل بارهای اضافی از بین می رود. در این بارگذاری ثابت، طول هر سه میله به صورت پلاستیک تغییر می کند.

به میزان بار در این حالت، «بار پلاستیک» (Plastic Load) گفته می شود. در منحنی بار-جابه جایی بالا، مختصات بار پلاستیک (PP) توسط نقطه B نمایش داده شده است. خط افقی BC نیز ناحیه تغییر شکل پلاستیک پیوسته در شرایط بارگذاری ثابت را نشان می دهد.

بار پلاستیک PP را می توان با استفاده از معادلات تعادل استاتیکی محاسبه کرد. برای این منظور در ابتدا معادلات زیر را در نظر می گیریم:

بر اساس معادلات تعادل داریم:

در نتیجه:

جابه جایی پلاستیک δP در لحظه رسیدن به بار پلاستیک PP، با تغییر طول میله های کناری در لحظه رسیدن به تنش تسلیم برابر است. در نتیجه:

با مقایسه δP و δY مشاهده می شود که در این مثال، نسبت جابه جایی پلاستیک به جابه جایی تسلیم به صورت زیر است:

به علاوه، نسبت بار پلاستیک به بار تسلیم نیز به صورت زیر است:

به طور کلی، نسبت جابه جایی ها همیشه بزرگ تر از نسبت بارهای به وجود آورنده آن ها و شیب خط AB در ناحیه نیمه پلاستیک منحنی بار-جابه جایی همیشه کوچک تر از شیب خط OA است.

علاوه بر این، کوچک ترین شیب منحنی نیز به بخش BC در ناحیه پلاستیک کامل تعلق دارد (شیب صفر).