تعریف تنش استوانه ای (Cylinder Stress)

تعریف تنش استوانه ای (Cylinder Stress):
«تنش استوانه ای» (Cylinder Stress)، نوعی توزیع تنش با تقارن چرخشی است. این نوع تنش در اجسام استوانه ای مشاهده می شود.

در این حالت، اگر جسم حول یک محور ثابت دوران کند، هیچ تغییری در توزیع تنش رخ نخواهد داد.

تنش استوانه ای شامل سه الگوی زیر می شود:

• «تنش حلقوی» (Hoop Stress) یا «تنش پیرامونی» (Circumferential Stress): نوعی تنش نرمال در جهت مماس بر نقطه مورد بررسی (تصویر زیر) است.
• «تنش محوری» (Axial Stress): نوعی تنش نرمال موازی با محور تقارن استوانه است.
• «تنش شعاعی» (Radial Stress): تنشی که با محور تقارن استوانه در یک صفحه قرار دارد اما بر آن محور عمود است.

یک مثال متداول و علت اصلی نام گذاری تنش حلقوی، نیروی کششی اعمال شده بر نوارهای فلزی یا حلقه های اطراف یک بشکه چوبی است.

در یک لوله مستقیم، اعمال نیروی های ناشی از اختلاف فشار به دیواره لوله، باعث افزایش تنش های حلقوی می شوند.

به طور مشابه، در صورتی که سرپوش دو انتهای لوله صاف باشد، نیروی اعمال شده ناشی از فشار استاتیک، یک تنش محوری عمود بر دیواره را ایجاد خواهد کرد. تنش شعاعی در مقاطع نازک، اغلب کوچک و قابل اغماض است.

با این وجود، برای مدل سازی دقیق ورقه های استوانه ای با جدار ضخیم باید این گونه تنش را در محاسبات مد نظر قرار داد.

تاریخچه توسعه تحلیل تنش استوانه ای:
اولین تحلیل تنش در اجسام استوانه ای توسط «ویلیام فیربرن» (William Fairbairn)، یکی از مهندسان عمران قرن 19 ام میلادی، با کمک «ایتن هاجکینسون» (Eaton Hodgkinson)، یکی از مهندسان پیشگام در زمینه به کارگیری تحلیل های ریاضی در طراحی سازه ها توسعه یافت. مطالعات اولیه این محققین بر روی طراحی و ارزیابی شکست دیگ های بخار صورت گرفت.

در طی این مطالعات، فیربرن متوجه شد که میزان تنش حلقوی دو برابر میزان تنش محوری (طولی) است و عامل مهمی در هنگام مونتاژ ورقه های دیگ بخار به حساب می آید.

این ورقه ها با استفاده از اتصال (پرچ کردن) ورقه های نورد شده به یکدیگر ساخته می شوند.

مطالعات بعدی در این زمینه، برای ساخت پل ها و اختراع «شاه تیر جعبه ای» (Box Girder) مورد استفاده قرار گرفتند.

در تصویر زیر، ستون های چدنی «پل چپستاو» (Chepstow Bridge) را مشاهده می کنید که توسط نوارهای بیرونی ساخته شده از آهنِ کار شده، تقویت شده اند. نیروی طولی و عمودی در این نوارها به صورت فشاری است و چدن قابلیت مقاومت در برابر این گونه نیرو را دارد.

از طرف دیگر، به دلیل مقاومت بیشتر آهنِ کار شده در برابر تنش حلقوی (نسبت به چدن)، این ماده نیز در اطراف ستون مورد استفاده قرار گرفته است.

تنش حلقوی:
تنش حلقوی، نیرویی است که به صورت محیطی (عمود بر راستای محور و شعاع جسم) به تمامی ذرات دیواره استوانه اعمال می شود. این تنش را می توان از طریق رابطه زیر بیان کرد:

F: نیروی محیطی اعمال شده بر سطح دیواره استوانه؛ t: ضخامت شعاعی استوانه؛ l: طول محوری استوانه

یکی از کمیت های جایگزین تنش حلقوی برای توصیف تنش محیطی، «تنش دیواره» (Wall Stress) یا «کشش دیواره» (Wall Tension) نام دارد. این کمیت به صورت نیروی محیطی در امتداد کل ضخامت شعاعی (طول استوانه) تعریف می شود.

T: تنش دیواره؛ F: نیروی محیطی؛ l: طول استوانه

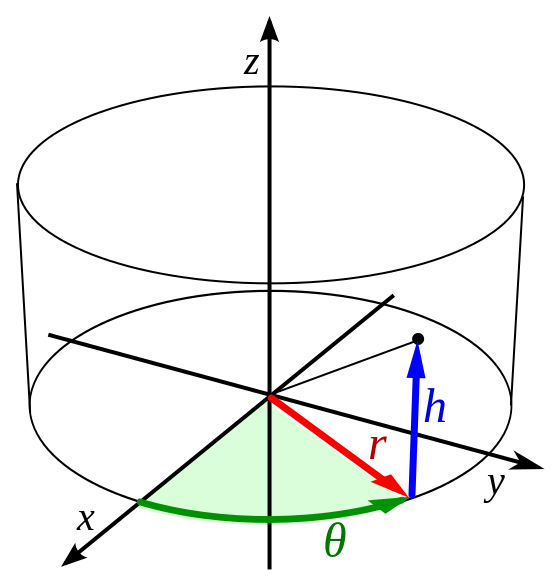
تنش های محوری و شعاعی به همراه تنش محیطی، مؤلفه های تانسور تنش در مختصات استوانه ای را نمایش می دهند (تصویر زیر). برای اجسام دارای تقارن چرخشی، تجزیه نیروهای اعمال شده به مؤلفه های موازی با مختصات استوانه ای z، r و θ به انجام بهتر محاسبات کمک می کند. این مؤلفه های نیرو به ترتیب باعث به ایجاد تنش های شعاعی، محوری و حلقوی می شوند.

رابطه بین فشار داخلی و تنش استوانه ای:
اجسام استوانه ای شکل با توجه به نسبت شعاع به ضخامت دیواره شان، به دو گروه «جدار نازک» (Thin-walled) و «جدار ضخیم» (Thick-walled) تقسیم می شوند. در ادامه به معرفی رابطه بین فشار داخلی و مولفه های تنش استوانه ای (تنش حلقوی، شعاعی و محوری) در این دو گروه می پردازیم.

استوانه جدار نازک:
استوانه ای که نسبت شعاع به ضخامت دیواره آن بیشتر از 10 (نسبت قطر به ضخامت کمتر از 20) باشد، استوانه جدار نازک به حساب می آید.

در این حالت می توان دیواره را به صورت یک سطح در نظر گرفت. به این ترتیب، تنش حلقوی ناشی از فشار داخلی بر روی یک استوانه نازک با استفاده از «معادله یانگ-لاپلاس» (Young-Laplace Equation) قابل محاسبه خواهد بود:

برای استوانه

برای کره

P: فشار داخلی؛ t: ضخامت دیواره؛ r: میانگین شعاع استوانه؛ σθ: تنش حلقوی

معادله تنش حلقوی در ورقه های نازک، برای پوسته های کروی نظیر سلول های گیاهی و باکتری ها نیز تقریباً معتبر است. برای به کارگیری اجسام استوانه ای نظیر لوله ها در مسائل مهندسی، رابطه تنش حلقوی بر اساس فشار بازنویسی می شود که به آن، «معادله بارلو» (Barlow’s Formula) می گویند.

در سیستم SI، فشار با واحد پاسکال (Pa) و ضخامت نیز مانند شعاع با واحد متر (m) بیان می شود. این واحدها در سیستم بریتانیایی به ترتیب، پوند بر اینچ مربع (psi) و اینچ (in) هستند.

در هنگام بسته بودن دو انتهای یک استوانه، اعمال فشار داخلی بر روی آن ها باعث ایجاد نیرویی در امتداد محور استوانه می شود. مقدار این نیرو بر واحد سطح، با عنوان تنش محوری شناخته می شود و معمولاً مقدار آن از تنش حلقوی کمتر است.

این تنش را می توان از طریق رابطه زیر نیز تخمین زد:

در این شرایط، علاوه بر تنش محوری یک تنش شعاعی (σr) نیز به وجود می آید که مقدار آن از طریق رابطه زیر برای استوانه جدار نازک قابل محاسبه است:

استوانه جدار ضخیم:
هنگامی که نسبت شعاع به ضخامت استوانه کمتر از 10 باشد (نسبت قطر به ضخامت کمتر از 20)، معادلات استوانه جدار نازک دیگر قابل استفاده نخواهند بود؛ چراکه در این حالت، مقدار تنش های بین سطوح داخلی و خارجی استوانه به صورت قابل توجهی تغییر می کند. به علاوه، تنش های برشی موجود مقاطع نیز قابل اغماض نیستند.

این تنش و کرنش ها را می توان با استفاده از «معادلات لامه» (Lamé Equations) محاسبه کرد. این معادلات توسط «گابریل لامه» (Gabriel Lamé)، ریاضیدان فرانسوی توسعه داده شده است.

A و B: ثابت های ادغام (از طریق شرایط مرزی تعیین می شوند)؛ r: شعاع نقطه مورد بررسی (بر روی بخش داخلی یا بیرونی دیواره)

A و B با استفاده از بررسی شرایط مرزی به دست می آیند. به عنوان مثال، این شرایط برای یک استوانه جامد (ساده ترین حالت) به صورت زیر است:

اگر Ri=0 باشد، B=0 خواهد بود. به این ترتیب، یک جسم استوانه ای جامد نمی توان دارای فشار داخلی باشد. بنابراین داریم: A=P0.

تأثیر تنش های حلوقی در حوزه های مختلف:
حال اجازه دهید مروری بر تأثیر تنش های حلقوی در حوزه های مختلف داشته باشیم.

مهندسی:
در اجسام استوانه ای اگر هیچ گونه بارگذاری خارجی بر روی جسم اعمال نشود، شروع شکستگی توسط تنش حلقوی کنترل خواهد شد.

تنش حلقوی در چنین وضعیتی بزرگ ترین تنش اصلی خواهد بود. توجه داشته باشید که در یک جسم حلقوی، کرنش کل در بخش داخلی و خارجی یکسان است اما به دلیل توزیع کرنش در شرایط مختلف، بیشترین تنش در بخش داخلی ظاهر می شود.

از این رو، بررسی وضعیت ایجاد و رشد ترک های یک لوله را باید از بخش داخلی آن شروع کرد. به همین دلیل، برای ارزیابی لوله ها پس از حوادثی مانند زمین لرزه، یک دوربین را به داخل لوله ارسال می شود تا ترک های داخلی مورد بررسی قرار گیرند.

تسلیم در اجسام استوانه ای توسط یک تنش معادل کنترل می شود. این تنش، ترکیبی از تنش حلقوی و طولی یا شعاعی (در صورت عدم وجود تنش طولی) است.

پزشکی:
در آسیب شناسی یا اصطلاحاً «پاتولوژی» (Pathology) دیواره رگ ها یا مجاری دستگاه گوارشی، کشش دیواره ها بیانگر کشش ماهیچه های دیواره رگ ها است.

با توجه به «قانون لاپلاس» (Law of Laplace)، اگر دیواره رگ های خونی دچار عارضه «آنوریسم» (Aneurysm) (بیرون زدگی و بزرگ شدن دیواره) شوند، شعاع رگ افزایش می یابد.

به این ترتیب، بر اثر کاهش نیروهای رو به داخل رگ، آنوریسم تا هنگام گسیختگی دیواره ها ادامه خواهد یافت.

تمام این فرآیندها برای عارضه «دیورتیکول» (Diverticuli) در روده نیز صادق هستند. بررسی نحوه عملکرد این مشکلات با استفاده از مفهوم تنش حلقوی صورت می گیرد.