تعریف معیارهای تنش در مکانیک محیط

تعریف معیارهای تنش در مکانیک محیط:
تنش یکی از مفاهیم اساسی و مهم در علوم مهندسی است و روش های متعددی برای تعریف و اندازه گیری تنش وجود دارد.

یکی از متداول ترین معیارهای تعیین تنش، «تانسور تنش کوشی» (Cauchy Stress Tensor) است که اغلب با عناوینی نظیر «تانسور تنش» (Stress Tensor) یا «تنش واقعی» (True Stress) شناخته می شود.

تصویر زیر را در نظر بگیرد. این تصویر، کمیت های مورد نیاز برای تعریف معیارهای تنش را نمایش می دهد.

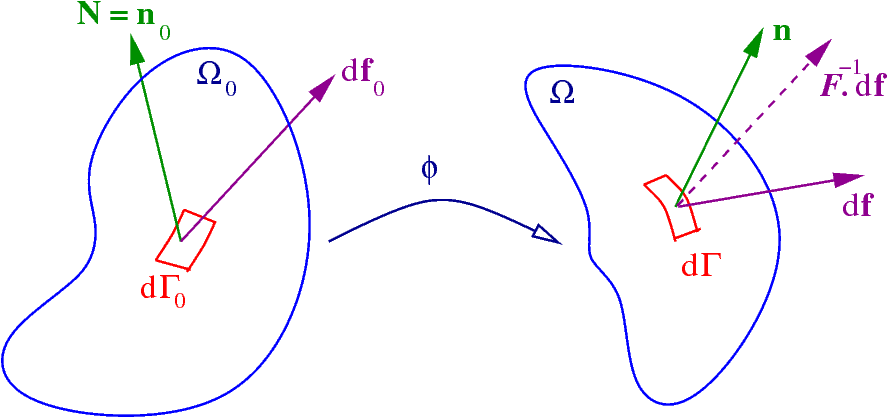
Ω0: پیکربندی مرجع (شکل اولیه)؛ dΓ0: المان سطح در پیکربندی مرجع؛ N≡n0: بردار نرمال المان سطح در پیکربندی مرجع؛ df0: بردار نیرو در پیکربندی مرجع؛ t0: بردار کشش اعمال شده بر روی dΓ0

Ω: پیکربندی تغییر یافته (شکل نهایی)؛ dΓ: المان سطح در پیکربندی تغییر یافته؛ n: بردار نرمال المان سطح در پیکربندی تغییر یافته؛ df: بردار نیرو در پیکربندی تغییر یافته؛ t: بردار کشش اعمال شده بر روی dΓ

توجه داشته باشید که سطوح مورد بررسی می توانند یا به صورت مقاطع فرضی درون جسم یا سطوح واقعی باشند. تانسور گرادیان تغییر شکل با F و دترمینان آن با J نمایش داده می شود.

تنش کوشی:
تنش کوشی یا تنش واقعی، معیاری برای نمایش نیروی اعمال شده بر یک المان سطح در پیکربندی تغییر یافته است. این تانسور به صورت متقارن بوده و توسط رابطه زیر تعریف می شود:

df=tdΓ=σT⋅ndΓ

یا

t=σT⋅nt=σT⋅n

تنش کیرشهف:
کمیت τ = J σ، به عنوان «تانسور تنش کیرشهف» (Kirchhoff Stress Tensor) شناخته می شود و کاربرد وسیعی در الگوریتم های عددی مورد استفاده برای شکل پذیری فلزات (تغییر شکل پلاستیک با حجم ثابت) دارد. نام دیگر این کمیت، «تانسور وزنی تنش کوشی» است.

تنش اسمی و تنش مرتبه اول پیولا-کیرشهف:
تنش اسمی (N = PT) ترانهاده «تنش مرتبه اول پیولا-کیرشهف» (First Piola-Kirchhoff Stress) است. تنش مرتبه اول پیولا-کیرشهف (P)، با عناوینی نظیر «تنش PK1» یا «تنش مهندسی» نیز شناخته می شود.

تنش اسمی به صورت زیر به دست می آید:

df=tdΓ=NT⋅n0dΓ0=P⋅n0dΓ0

یا

t0=tdΓdΓ0=NT⋅n0=P⋅n0

این تنش به صورت نامتقارن بوده و همانند گرادیان تغییر شکل، یک تانسور دو نقطه ای است. عدم تقارن این تانسور از اختصاص یک شاخص به پیکربندی مرجع و یک شاخص به پیکربندی تغییر یافته نشات می گیرد.

تنش مرتبه دوم پیولا-کیرشهف:
اگر موقعیت مکانی df را به پیکربندی مرجع انتقال دهیم (عملیات پول بَک)، خواهیم داشت:

df0=F−1⋅df
یا

df0=F−1⋅NT⋅n0dΓ0=F−1⋅t0dΓ0

به این ترتیب، «تنش مرتبه دوم پیولا-کیرشهف» (Second Piola-Kirchhoff Stress) به صورت زیر تعریف خواهد شد:

df0=ST⋅n0dΓ0=F−1⋅t0dΓ0

در نتیجه داریم:

ST⋅n0=F−1⋅t0

تنش بیو:
«تنش بیو» (Biot Stress)، مزدوج انرژیِ تانسور کشش راست (U) یا تانسور کشش ماده است. این تنش، به عنوان بخش متقارن تانسور PT.R تعریف می شود. R، تانسور دوران را نشان می دهد که از تجزیه قطبی گرادیان تغییر شکل به دست می آید.

از این رو، تانسور تنش بیو به صورت زیر خواهد بود:

T=12(RT⋅P+PT⋅R)

تنش بیو با عنوان «تنش جائومن» (Jaumann Stress) نیز شناخته می شود. کمیت T، دارای مفهوم فیزیکی نیست.

با ان وجود، تنش نامتقارن بیو به صورت زیر تعریف خواهد شد:

RTdf=(PT⋅R)T⋅n0dΓ0