تعریف کنترل مقاوم در صنعت برق

تعریف کنترل مقاوم:
نظریه کنترل رایج و متعارف به بشر این امکان را داده است تا قرن ها محیط خود را کنترل و خودکار کند. با گذشت زمان، تکنیک های کنترل مدرن به مهندسان این توانایی را داده است که سیستم های کنترلی را که از نظر هزینه و کارایی بهینه کنند.

با این حال، الگوریتم های کنترل بهینه همیشه در برابر تغییرات سیستم کنترل یا محیط کارایی لازم را ندارند. نظریه «کنترل مقاوم» (Robust Control) راهکاری برای اندازه گیری تغییرات عملکرد یک سیستم کنترل نسبت به تغییر پارامترهای سیستم و کنترل آن است.

استفاده از این تکنیک برای ساختن «سیستم های توکار یا تعبیه ای» (Embedded Systems) قابل اعتماد اهمیت فراوانی دارد. هدف کنترل مقاوم این است که امکان کاوش در فضای طراحی برای گزینه های غیرحساس نسبت به تغییرات در سیستم فراهم شود و بتواند پایداری و عملکرد آن ها را حفظ کند.

یکی از نتایج مطلوب این روش، مربوط به سیستم هایی است که در صورت وجود تغییرات یا خطاهای سیستم، افت عملکرد شدیدی را نشان می دهند.

چرا کنترل مقاوم؟
برای بررسی کنترل مقاوم یک روش مفید این است که از برخی مفاهیم اساسی نظریه کنترل استفاده کنیم. نظریه کنترل از نظر تاریخی به دو بخش تقسیم می شود:

کنترل سنتی یا کلاسیک و کنترل مدرن. کنترل کلاسیک مفاهیم و روش هایی را پوشش می دهد که تا سال 1950 رایج بودند. کنترل مدرن به روش های ارائه شده از 1950 تاکنون اطلاق می شود. در ادامه، درباره این دو دسته به اختصار بحث می کنیم.

کنترل کلاسیک با گسترش نظریه فیدبک مورد توجه قرار گرفت. از فیدبک برای پایدارسازی سیستم کنترل استفاده شد. یکی از اولین استفاده ها از کنترل فیدبک تنظیم گر گریز از مرکز برای پایدارسازی موتورهای بخار لوکوموتیوها بود.

نمونه دیگر استفاده از فیدبک، در سیگنال های تلفن در دهه 1920 بود. مسئله موجود، انتقال سیگنال ها از طریق خطوط طولانی بود. در تعداد تکرارگرها محدودیت وجود داشت که به دلیل اعوجاج، به صورت سری با خط تلفن اضافه می شدند.

«هارولد استفن بلک» (Harold Stephen Black) سیستم فیدبکی را پیشنهاد داد که از فیدبک برای محدود کردن اعوجاج بهره می برد. حتی اگر فیدبک اضافه شده باعث افزایش بهره تکرارگر می شد، اما عملکرد کلی را ارتقا می بخشید.

کنترل کلاسیک مبتنی بر تشکیل یک مدل از سیستم کنترل با استفاده از معادلات دیفرانسیل است. از تبدیل لاپلاس برای بیان معادلات سیستم در فضای فرکانس استفاده می شود. در این فضا، می توان عملیات جبری را به سادگی روی معادلات انجام داد.

شکل 1 یک حلقه کنترل رایج را نشان می دهد. ورودی سیستم سیگنال مرجع است که مقدار کنترل مطلوب را نشان می دهد. این مرجع به تابع تبدیل پیش رویG(s) اصطلاحاً خورانده می شود تا خروجی y دستگاه تعیین شود. خروجی از طریق تابع تبدیلH(s) بازخورانده (فیدبک) می شود.

سیگنال فیدبک از مرجع کم شده و سیگنال خطای e به دست می آید. کنترل آتی بر اساس سیگنال خطا است.

بنابراین، سیستم به گونه ای عمل می کند که خروجی تا حد ممکن به ورودی مرجع مطلوب نزدیک شود. به دلیل پیچیدگی ریاضیات، روش های کنترل کلاسیک اغلب در سیستم های تک خروجی-تک ورودی (SISO) به کار می رفتند.

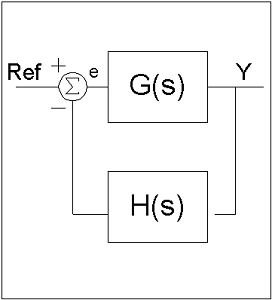
شکل 1: حلقه کنترل رایج

یکی از پیشرفت های مهم در گسترش کنترل مقاوم، روش مکان هندسی ریشه ها بود. در حوزه فرکانس، G(s)وH(s) به عنوان نسبت چندجمله ای هایی بر حسب متغیر فرکانس مختلط s بیان شدند. «نایکوئیست» (Nyquist)، «بود» (Bode) و دیگران فهمیدند که ریشه های چندجمله ای مخرج، پایداری سیستم کنترل را مشخص می کنند.

به این ریشه ها «قطب» تابع تبدیل گفته می شود. موقعیت این قطب ها برای تضمین پایداری باید در نیم صفحه چپ صفحه فرکانس مختلط باشد. مکان ریشه روشی گرافیکی برای نشان دادن حرکت قطب ها در دامنه فرکانس در اثر تغییر ضرایب چندجمله ای s است.

حرکت به سمت نیمه راست صفحه به معنای سیستمی ناپایدار است. بنابراین سیستم ها را می توان با حساسیت آن ها به تغییرات کوچک در ضرایب مخرج مورد بررسی قرار داد.

روش های کنترل مدرن با تحقق معادلات سیستم کنترل توسعه یافتند، به گونه ای که کامپیوترها می توانستند آن ها را به خوبی حل کنند.

نشان داده شد که هر معادله دیفرانسیل مرتبه n اُم که سیستم کنترل را توصیف می کرد، قابلیت تبدیل به n معادله مرتبه اول را دارد. این معادلات را می توان به فرم معادلات ماتریسی نوشت.

این روش اغلب یه عنوان روش متغیر حالت شناخته می شود. فرم کانونی معادلات حالت در ادامه نشان داده شده است که در آن، →x برداری است که حالت سیستم را نشان می دهد، ˙→x بردار تغییر حالت، uبردار ورودی ها، y بردار خروجی ها وA، B، C وD ماتریس هایی هستند که به سیستم کنترل بستگی دارند.

روش های کنترل مدرن بسیار موفق بوده اند، زیرا به خوبی در کامپیوتر قابل پیاده سازی هستند، با سیستم های چندورودی-چندخروجی (MIMO) سازگاری دارند و می توان آن ها را بهینه کرد.

روش های بهینه کردن ماتریس های حالت ثابت توسعه یافته بود و برای مثال، یک سیستم کنترل فضاپیما برای رسیدن به مقصد در کوتاه ترین زمان یا با مصرف حداقل مقدار سوخت یا ترکیبی وزن دار از این دو بهینه شد.

قابلیت طراحی برای عملکرد و هزینه مطلوب، سیستم های کنترل مدرن را بسیار محبوب کرده است.

کنترل مقاوم به کنترل دستگاه های نامعلوم با دینامیک نامعلوم ناشی از اغتشاش های نامعلوم اطلاق می شود.

واضح است که مسئله اصلی سیستم های کنترل مقاوم نامعینی و چگونگی برخورد سیستم کنترل با این مشکل است. شکل 2 نمایی از حلقه کنترل ساده ای است که در بالا نشان دادیم. نامعینی وارد بر سیستم در سه مکان نشان داده شده است.

در مدل دستگاه، نامعینی وجود دارد. اغتشاش هایی وجود دارد که در سیستم رخ می دهد. همچنین نویزهایی وجود دارد که در ورودی های سنسور خوانده می شود. هر کدام از این نامعینی ها می توانند یک مؤلفه جمع شونده یا ضرب شونده داشته باشد.

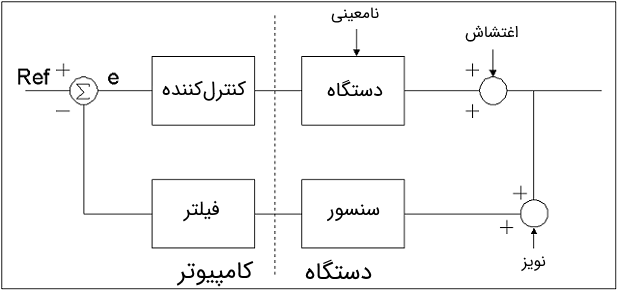
شکل 2: حلقه کنترل دستگاه با نامعینی

شکل بالا همچنین جدایی سیستم کنترل کامپیوتری را از دستگاه نشان می دهد. درک این نکته مهم است که طراح سیستم کنترل، کنترل اندکی روی نامعینی سیستم دارد.

طراح، یک سیستم کنترل طراحی می کند که مبتنی بر مدل دستگاه است. البته سیستم کنترل پیاده شده باید با سیستم واقعی تعامل داشته باشد، نه با مدل آن.