تعریف تابع انتقال حلقه قفل فاز

تعریف تابع انتقال حلقه قفل فاز:

در تصویر زیر یک دیاگرام دیگر از حلقه قفل فاز را می توان مشاهده کرد.

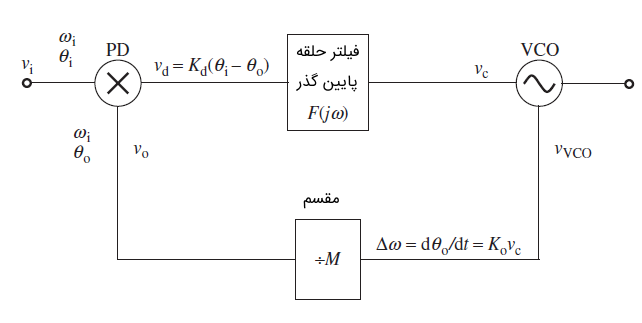
زمانی که دو ورودی، سیگنال هایی کوچک باشند، آشکارساز فاز در این مدار یک ضرب کننده خواهد بود. دو سیگنال ورودی را به صورت زیر فرض می کنیم:

در روابط فوق، vi سیگنال ورودی به آشکارساز فاز، vo ورودی دوم آشکارساز فاز از مدار مقسم، ωi فرکانس سیگنال ورودی، θi فاز سیگنال ورودی وθo فاز سیگنال خروجی از مقسم هستند.

معادله اساسی حلقه در دیاگرام فوق به صورت زیر به دست می آید:

که در این رابطه، Km برابر با فاکتور ضرب در ضرب کننده با ابعاد[V−1] است.

به دلیل وجود فیلتر پایین گذر در حلقه، می توان از فرکانس های بالا در روابط صرف نظر کرد و رابطه را به صورت زیر بازنویسی کرد.

تغییرات فاز در خروجی مدار اسیلاتور کنترل شده با ولتاژ به صورت خطی با ولتاژ کنترل در ورودی VCO متناسب است. بنابراین می توان نوشت:

که در این فرمول، K0 برابر با فاکتور بهره اسیلاتور کنترل شده با ولتاژ وM مرتبه تقسیم مقسم است. با استفاده از نوتیشن لاپلاس، معادلات اساسی حلقه را می توان به صورت زیر بازنویسی کرد:

تابع تبدیل حلقه باز یا بهره حلقه باز به صورت زیر محاسبه می شود:

اختلاف فاز بین دو سیگنال ورودی به آشکارساز فاز را باθe نشان می دهیم و به صورت زیر آن را محاسبه می کنیم:

تابع انتقال حلقه بسته حلقه قفل فاز به صورت زیر به دست می آید:

ولتاژ ورودی به اسیلاتور کنترل شده با ولتاژ را می توان به طریق زیر به دست آورد:

در حلقه قفل فاز معمولا فیلتر حلقه پایین گذر، یک فیلتر پسیو یا یک فیلتر اکتیو مرتبه دوم است. در تصویر زیر می توان شماتیک این دو فیلتر را مشاهده کرد.

تابع انتقال یک فیلتر پسیو که در شکل سمت چپ نشان داده شده است را می توان به صورت زیر نوشت:

که در آن داریم:

تابع انتقال مربوط به یک فیلتر اکتیو که در شکل سمت راست تصویر فوق دیده می شود را نیز می توان به صورت زیر نوشت:

اگرA≫1 باشد، آن گاه داریم:

در رابطه فوق موارد زیر برقرار هستند:

تابع انتقال حلقه بسته فیلتر پسیو و اکتیو مرتبه دوم به صورت زیر به دست می آید. برای فیلتر پسیو می توان نوشت:

و برای فیلتر اکتیو مرتبه دوم نیز داریم:

این دو تابع انتقال حلقه بسته را می توان به این صورت بازنویسی کرد:

که در آنωnp برابر با فرکانس طبیعی حلقه وζp برابر با فاکتور میرایی هستند. در نتیجه می توان روابط زیر را برای فیلتر پسیو نوشت:

همچنین برای فیلتر اکتیو مرتبه دوم روابط زیر برقرار هستند: