خانه
اپلیکیشن زینگ
آشنایی و همکاری
سامانه صادرات و واردات
فروشگاه
خدمات اطلاعاتی
اخبار و مقالات
تماس با ما


معادلات حالت در مدار:
معادلات حالت در مدار یکی از روش های بسیار مهم برای تجزیه و تحلیل مدارات پیچیده و مدارات دارای چند ورودی و چند خروجی است.

اکثر روش های تحلیل مدار برای آنالیز مدارات با یک ورودی و یک خروجی کاربرد دارند. اما در بسیاری از سیستم های مهندسی تعداد زیادی ورودی و خروجی وجود دارند.
معادلات حالت یا مدل متغیر حالت، نسبت به مدل تک ورودی-تک خروجی بسیار عمومی تر است. در مدل متغیر حالت، مجموعه ای از متغیرها را مشخص می کنیم، که توصیف کننده رفتار داخلی سیستم هستند.
این متغیرها به عنوان متغیرهای حالت سیستم شناخته می شوند و می توانند تعیین کننده رفتار آینده سیستم، در صورت مشخص بودن حالت های سیستم و ورودی آن باشند.
به عبارت دیگر اگر متغیرهای حالت مشخص باشند، اجازه می دهند که سایر متغیرهای سیستم فقط با استفاده از معادلات جبری به دست آیند. متغیر حالت یک مشخصه فیزیکی است که حالت سیستم را بدون توجه به این که سیستم چگونه به آن نقطه رسیده است، مشخص می کند.
فشار، حجم و دما، مثال های متداول متغیرهای حالت هستند. در یک مدار الکتریکی، جریان سلف ها و ولتاژ خازن ها به عنوان متغیرهای حالت انتخاب می شوند. زیرا این متغیرها می توانند وضعیت انرژی سیستم را توصیف کنند.
آسان ترین راه برای نمایش معادلات فضای حالت، چیدن آن ها به صورت مجموعه ای از معادلات دیفرانسیل مرتبه اول به صورت زیر است:
x=Ax+Bz
در فرمول بالا x بردار حالت های سیستم از مرتبه n است و از تمام متغیرهای حالت سیستم تشکیل شده است.
اگر˙x نشان دهنده مشتق مرتبه اول متغیرهای حالت نسبت به زمان باشد، در نتیجه داریم:
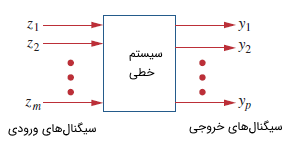
همچنین بردار ورودی های سیستم به ازای m ورودی، به صورت زیر است:
A و B به ترتیب هر کدام ماتریس های n×n و n×m هستند. علاوه بر معادله بالا، به معادله خروجی هم نیاز داریم. در نتیجه معادلات فضای حالت کامل به صورت زیر نوشته می شود:
که در فرمول بالا y بردار خروجی های سیستم و به صورت زیر است:
همچنین ماتریس های C و D به ترتیب دارای ابعاد p×n و p×m هستند. برای موارد خاصی که سیستم تک ورودی-تک خروجی باشد، n=m=p=1 است.
با فرض شرایط اولیه صفر، تابع انتقال سیستم از طریق تبدیل لاپلاس گرفتن از معادله حالت، به صورت زیر به دست می آید:
فرمول بالا را می توان به فرم زیر نیز نوشت:
که در این فرمول، I ماتریس همانی است. حال از معادله به دست آمده برای خروجی سیستم نیز تبدیل لاپلاس می گیریم.
حال تابع انتقال سیستم از طریق تقسیم کردن تبدیل لاپلاس خروجی بر تبدیل لاپلاس ورودی به صورت زیر به دست می آید:
در فرمول بالا، A ماتریس سیستم، B ماتریس کوپل ورودی، C ماتریس خروجی و D ماتریس فیدبک هستند. در اکثر موارد ماتریس D برابر با صفر است. بنابراین درجه صورت H(S) کمتر از مخرج آن است. برای محاسبه تابع انتقال یک مدار می توان از نرم افزار MATLAB نیز استفاده کرد.
در حالت کلی برای آنالیز متغیر حالت، سه گام زیر را می توان در نظر گرفت.