تعریف مسئله در قالب ماتریس ها

تعریف مسئله در قالب ماتریس ها:
در این بخش، دانش خود درباره حالت را به عنوان یک حباب یا توده گوسی (Gaussian blob) مدل می کنیم. بنابراین، به یک اطلاعات دوبخشی در زمان k نیاز داریم.

بهترین تخمین راˆxkمی نامیم (که همان میانگین μ است) و ماتریس کوواریانس Pk را به صورت زیر می نویسیم:

توجه کنید که در اینجا، فقط سرعت و موقعیت را در نظر گرفته ایم و بردار حالت می تواند هر تعداد متغیر حالت داشته باشد.

اکنون باید حالت فعلی (در زمانk−1) و پیش بینی حالت بعدی در زمان k را تعیین کنیم. لازم به یادآوری است که اطلاعی نداریم کدام حالت واقعی است، اما این موضوع تأثیری در عملکرد پیش بینی ندارد؛ زیرا پیش بینی با همه آن ها کار می کند و توزیع جدیدی را نتیجه خواهد داد.

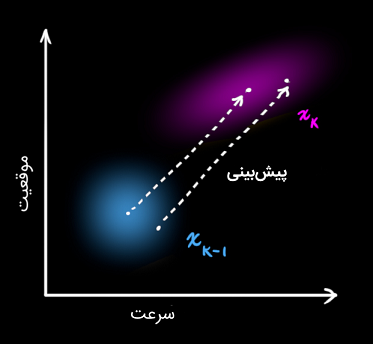
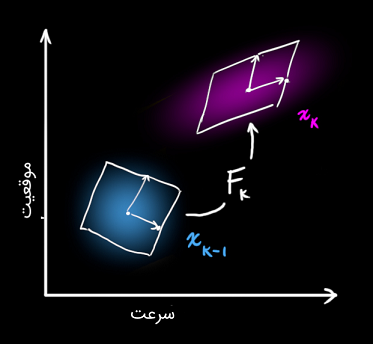
مرحله پیش بینی را با ماتریس Fk نمایش می دهیم.

پیش بینی برای هر نقطه از تخمین اولیه (Original) انجام می شود و آن را به یک محل پیش بینی شده جدید انتقال می دهد.

اکنون بررسی می کنیم که چگونه باید از یک ماتریس برای پیش بینی موقعیت و سرعت در لحظه بعدی استفاده کنیم. از فرمول پایه ای سینماتیک زیر استفاده می کنیم:

به عبارت دیگر:

اکنون یک ماتریس پیش بینی داریم که حالت بعدی را به دست می دهد، اما هنوز نمی دانیم ماتریس کوواریانس را چگونه به روز کنیم.

حال به یک فرمول دیگر نیاز داریم. فکر می کنید اگر هر نقطه در توزیع را در یک ماتریس A ضرب کنیم، ماتریس کوواریانس Σ چه تغییری خواهد کرد؟

ویژگی زیر را برای کوواریانس داریم:

با ترکیب رابطه (4) با (3)، به فرمول های زیر می رسیم: